ernanhughes

+++ date = ‘2025-01-17T18:07:50Z’ draft = true title = ‘43 Machine Learning Questions and Answers with Python examples’ +++

1. What is overfitting, and how can you prevent it in machine learning?

Answer: Overfitting occurs when a model learns the noise and details in the training data to the extent that it negatively impacts the model’s performance on new data. It essentially “memorizes” the training data instead of learning the underlying patterns.

Prevention Methods:

Python Example:

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score

# Generate a toy classification dataset
X, y = make_classification(n_samples=1000, n_features=20, random_state=42)

# Split data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Initialize the model
model = LogisticRegression(max_iter=10000)

# Perform cross-validation to check for overfitting
scores = cross_val_score(model, X_train, y_train, cv=5)
print(f'Cross-validation scores: {scores}')
print(f'Mean cross-validation score: {scores.mean()}')

Cross-validation scores: [0.85625 0.875   0.85625 0.86875 0.88125]
Mean cross-validation score: 0.8674999999999999

2. What is the difference between supervised and unsupervised learning?

Answer:

Supervised Learning Example: Regression (Predicting House Prices)

In this example, we’ll use a simple linear regression model to predict house prices based on some features like the size of the house.

Python Code for Regression:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_regression

# Generate some synthetic data for regression (house size vs price)
X, y = make_regression(n_samples=100, n_features=1, noise=10, random_state=42)

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Initialize the Linear Regression model
model = LinearRegression()

# Train the model on the training data
model.fit(X_train, y_train)

# Make predictions on the test set
y_pred = model.predict(X_test)

# Plot the results
plt.scatter(X_test, y_test, color='blue', label='Actual Prices')
plt.plot(X_test, y_pred, color='red', label='Predicted Prices')
plt.title('Regression: House Price Prediction')
plt.xlabel('House Size (sq ft)')
plt.ylabel('Price ($)')
plt.legend()
plt.show()

# Print model performance
print(f'Model Coefficients: {model.coef_}')
print(f'Model Intercept: {model.intercept_}')

Results

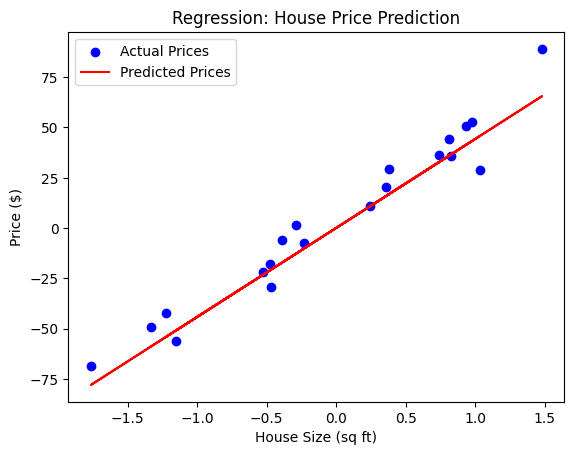
Regression

Explanation:

Supervised Learning Example: Classification (Iris Flower Classification)

In this example, we’ll use the k-Nearest Neighbors (k-NN) classifier to classify the species of an iris flower based on its features.

Python Code for Classification:

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score

# Load the Iris dataset
iris = load_iris()
X, y = iris.data, iris.target

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Initialize the k-NN classifier
knn = KNeighborsClassifier(n_neighbors=3)

# Train the classifier on the training data
knn.fit(X_train, y_train)

# Make predictions on the test set
y_pred = knn.predict(X_test)

# Evaluate the model performance
print(f'Accuracy: {accuracy_score(y_test, y_pred)}')

# Show the classification results
print(f'Predicted Classes: {y_pred}')
print(f'Actual Classes: {y_test}')

Accuracy: 1.0
Predicted Classes: [1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0 0 0 1 0 0 2 1
 0 0 0 2 1 1 0 0]
Actual Classes: [1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0 0 0 1 0 0 2 1
 0 0 0 2 1 1 0 0]

Explanation:

Key Differences Between Regression and Classification:

  1. Regression:
    • Predicts continuous numerical values.
    • Example: Predicting house prices.
    • Common models: Linear Regression, Decision Trees (for regression), Random Forest (for regression).
  2. Classification:
    • Predicts discrete class labels.
    • Example: Classifying flowers into species.
    • Common models: Logistic Regression, k-NN, Support Vector Machines (SVM), Decision Trees (for classification), Random Forest (for classification).

Unsupervised Learning example: Clustering with K-Means:

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# Create a toy dataset for clustering
X, _ = make_blobs(n_samples=500, centers=4, random_state=42)

# Apply KMeans clustering
kmeans = KMeans(n_clusters=4, random_state=42)
y_kmeans = kmeans.fit_predict(X)

# Visualize the clusters
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, cmap='viridis')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=200, c='red', marker='X')
plt.title("K-Means Clustering")
plt.show()

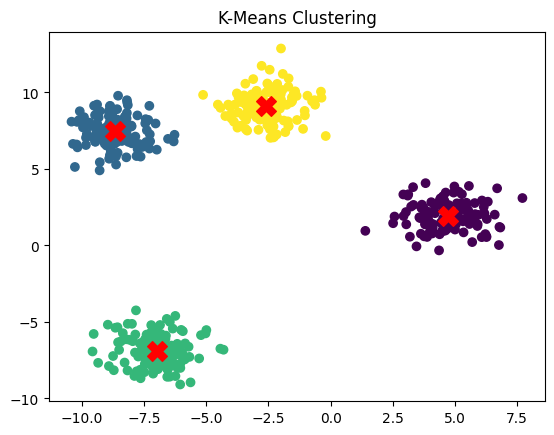
Clustering

3. What is cross-validation, and why is it important?

Answer: Cross-validation is a technique used to evaluate the performance of a machine learning model by partitioning the data into multiple subsets (folds). The model is trained on some folds and tested on the remaining fold, and this process is repeated several times to obtain an average performance score.

Why is it important? It helps to reduce overfitting, gives a more reliable estimate of model performance, and makes better use of limited data.

Python Example:

from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris

# Load dataset
X, y = load_iris(return_X_y=True)

# Initialize the model
model = RandomForestClassifier()

# Perform cross-validation
scores = cross_val_score(model, X, y, cv=5)
print(f'Cross-validation scores: {scores}')
print(f'Mean accuracy: {scores.mean()}')

Results

Cross-validation scores: [0.96666667 0.96666667 0.93333333 0.96666667 1.        ]
Mean accuracy: 0.9666666666666668

4. What is regularization, and what types of regularization are commonly used?

Answer: Regularization is a technique used to prevent overfitting by adding a penalty term to the model’s loss function. It discourages the model from fitting overly complex models that may overfit the data.

Python Example:

from sklearn.linear_model import Ridge, Lasso
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt

# Generate a regression dataset
X, y = make_regression(n_samples=100, n_features=1, noise=0.5, random_state=42)

# Fit Ridge and Lasso models with regularization
ridge = Ridge(alpha=1.0)
lasso = Lasso(alpha=0.1)

ridge.fit(X, y)
lasso.fit(X, y)

# Plot the results
plt.scatter(X, y, label='Data')
plt.plot(X, ridge.predict(X), label='Ridge Regression', color='r')
plt.plot(X, lasso.predict(X), label='Lasso Regression', color='g')
plt.legend()
plt.show()

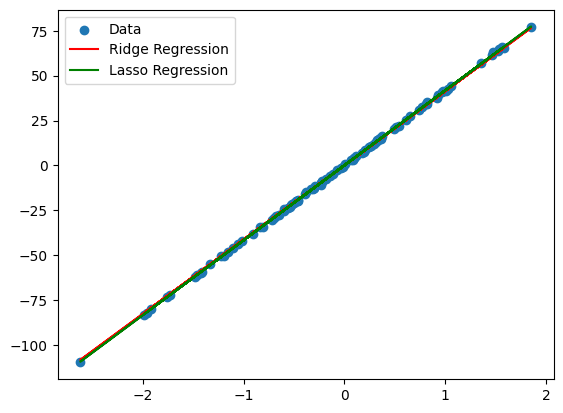
Regularization

5. What is the bias-variance tradeoff?

Answer: The bias-variance tradeoff is the balance between two sources of error that affect machine learning models:

The goal is to find a model that generalizes well and has low bias and variance.

Python Example:

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score

# Generate a simple classification dataset
X, y = make_classification(n_samples=1000, n_features=20, random_state=42)

# Split into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Logistic Regression (high bias, low variance)
logreg = LogisticRegression()
logreg.fit(X_train, y_train)
y_pred_logreg = logreg.predict(X_test)
logreg_accuracy = accuracy_score(y_test, y_pred_logreg)

# Decision Tree (low bias, high variance)
dtree = DecisionTreeClassifier()
dtree.fit(X_train, y_train)
y_pred_dtree = dtree.predict(X_test)
dtree_accuracy = accuracy_score(y_test, y_pred_dtree)

print(f"Logistic Regression accuracy: {logreg_accuracy}")
print(f"Decision Tree accuracy: {dtree_accuracy}")

Logistic Regression accuracy: 0.855
Decision Tree accuracy: 0.845

6. What are decision trees, and how do they work?

Answer: A decision tree is a supervised learning algorithm used for classification and regression. It splits the data into subsets based on the feature values, creating a tree-like structure of decisions and outcomes.

Python Example:

from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.datasets import load_iris

# Load dataset
X, y = load_iris(return_X_y=True)

# Fit a decision tree classifier
dtree = DecisionTreeClassifier(random_state=42)
dtree.fit(X, y)

# Plot the decision tree
plt.figure(figsize=(12, 8))
plot_tree(dtree, filled=True, feature_names=load_iris().feature_names, class_names=load_iris().target_names)
plt.show()

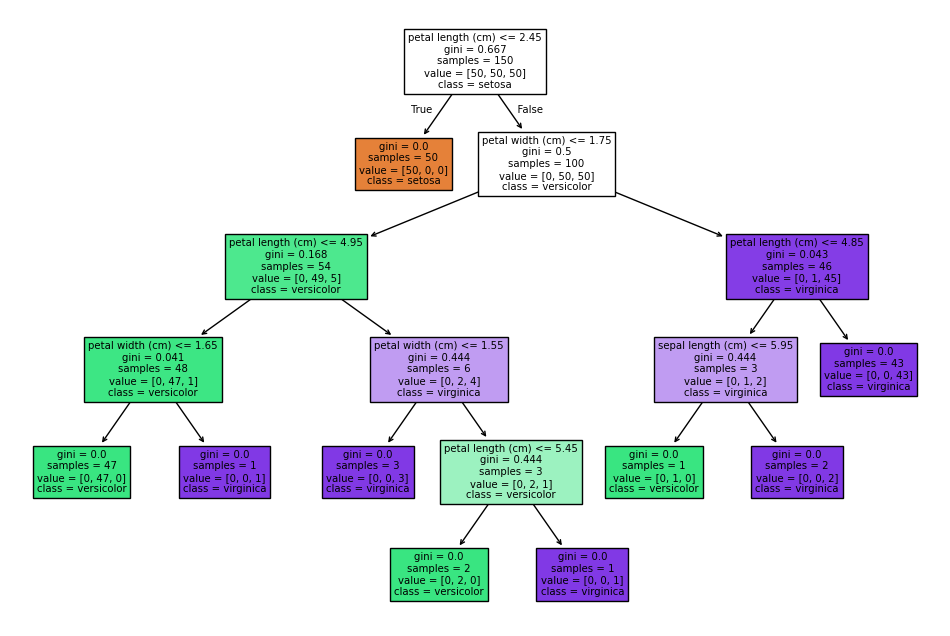
Decision Tree

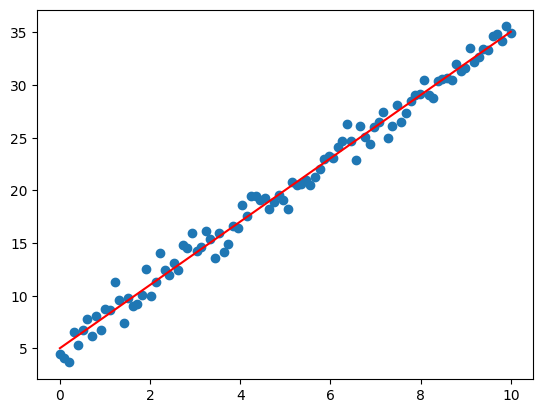
7. What is gradient descent?

Answer: Gradient descent is an optimization algorithm used to minimize the loss function by iteratively moving towards the minimum value of the function. It is widely used for training machine learning models, especially neural networks.

Python Example (Linear Regression):

import numpy as np
import matplotlib.pyplot as plt

# Generate some data
X = np.linspace(0, 10, 100)
y = 3 * X + 5 + np.random.randn(100)  # y = 3x + 5 with noise

# Initialize parameters
m = 0  # Slope (weight)
b = 0  # Intercept (bias)
learning_rate = 0.01
epochs = 1000

# Gradient Descent loop
for _ in range(epochs):
    y_pred = m * X + b
    error = y_pred - y
    m_gradient = (2 / len(X)) * np.dot(error, X)  # Derivative with respect to m
    b_gradient = (2 / len(X)) * np.sum(error)  # Derivative with respect to b
    m -= learning_rate * m_gradient
    b -= learning_rate * b_gradient

# Plotting the result
plt.scatter(X, y)
plt.plot(X, m * X + b, color='red')
plt.show()

Gradient Descent

8. What is the “curse of dimensionality”?

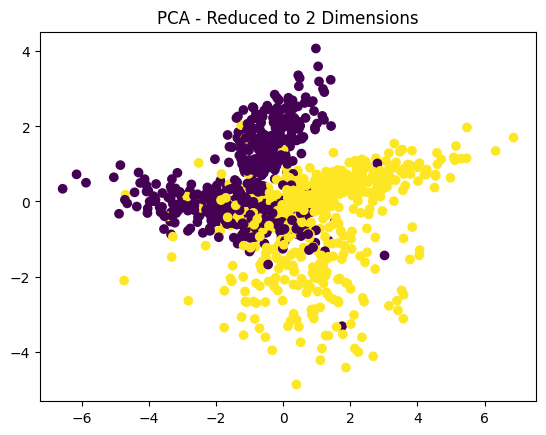
Answer: The “curse of dimensionality” refers to the exponential increase in computational complexity and data sparsity as the number of features (dimensions) grows. In high-dimensional spaces, distances between data points become less meaningful, making clustering and classification algorithms less effective.

Python Example (PCA for Dimensionality Reduction):

from sklearn.decomposition import PCA
from sklearn.datasets import make_classification

# Create a high-dimensional dataset
X, y = make_classification(n_samples=1000, n_features=50, random_state=42)

# Apply PCA to reduce dimensions
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X)

# Plot the reduced data
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y, cmap='viridis')
plt.title("PCA - Reduced to 2 Dimensions")
plt.show()

PCA

9. How do you evaluate the performance of a classification model?

Answer: The performance of a classification model can be evaluated using several metrics, including:

Python Example:

from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris

# Load dataset
X, y = load_iris(return_X_y=True)

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Train a model
model = LogisticRegression(max_iter=10000)
model.fit(X_train, y_train)

# Make predictions
y_pred = model.predict(X_test)

# Evaluate performance
print(classification_report(y_test, y_pred))

Classification Report

             precision    recall  f1-score   support

           0       1.00      1.00      1.00        10
           1       1.00      1.00      1.00         9
           2       1.00      1.00      1.00        11

    accuracy                           1.00        30
   macro avg       1.00      1.00      1.00        30
weighted avg       1.00      1.00      1.00        30

10. What is ensemble learning?

Answer: Ensemble learning is a technique where multiple models (often of the same type) are combined to make predictions, improving accuracy and robustness. Common ensemble methods include:

Python Example (Random Forest):

from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Load dataset
X, y = load_iris(return_X_y=True)

# Split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Train RandomForest model
rf = RandomForestClassifier(n_estimators=100)
rf.fit(X_train, y_train)

# Make predictions
y_pred = rf.predict(X_test)

# Evaluate the model
print(f"Accuracy: {accuracy_score(y_test, y_pred)}")

Accuracy: 1.0

11. What is the difference between classification and regression?

Answer:

Python Example (Classification and Regression):

# Classification example
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Classification model
classifier = LogisticRegression(max_iter=10000)
classifier.fit(X_train, y_train)
y_pred_class = classifier.predict(X_test)
print(f'Classification Accuracy: {accuracy_score(y_test, y_pred_class)}')

# Regression example
from sklearn.datasets import make_regression
from sklearn.linear_model import LinearRegression

X_reg, y_reg = make_regression(n_samples=100, n_features=1, noise=0.1, random_state=42)
X_train_reg, X_test_reg, y_train_reg, y_test_reg = train_test_split(X_reg, y_reg, test_size=0.3, random_state=42)

# Regression model
regressor = LinearRegression()
regressor.fit(X_train_reg, y_train_reg)
y_pred_reg = regressor.predict(X_test_reg)
print(f'Regression R^2: {regressor.score(X_test_reg, y_test_reg)}')

Classification Accuracy: 1.0
Regression R^2: 0.9999930887851615

12. What are the different types of gradient descent algorithms?

Answer:

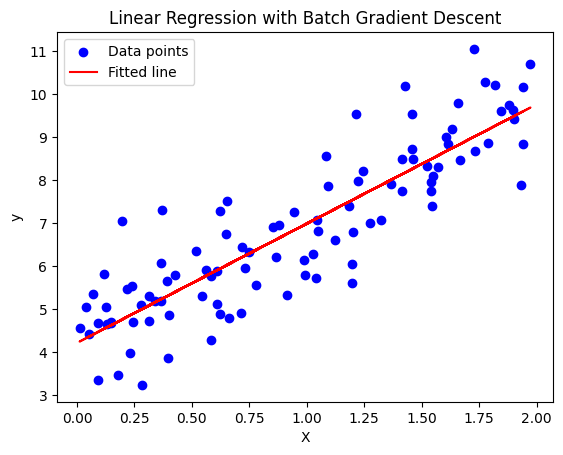
Batch Gradient Descent Algorithm:

  1. Initialize the parameters (weights).
  2. Compute the prediction for all training data.
  3. Compute the cost function (mean squared error).
  4. Calculate the gradients of the cost function with respect to each parameter.
  5. Update the parameters (weights) by moving them in the direction of the negative gradient.
  6. Repeat the process until convergence (i.e., when the cost function stops changing significantly).

Python Code for Batch Gradient Descent:

import numpy as np
import matplotlib.pyplot as plt

# Generate synthetic data (y = 2 * X + 1 + noise)
np.random.seed(42)
X = 2 * np.random.rand(100, 1)  # Random feature between 0 and 2
y = 4 + 3 * X + np.random.randn(100, 1)  # y = 4 + 3X + noise

# Add an extra column of ones to X for the intercept (bias term)
X_b = np.c_[np.ones((100, 1)), X]  # Add x0 = 1 for each instance

# Hyperparameters
learning_rate = 0.1  # Learning rate
n_iterations = 1000  # Number of iterations
m = len(X_b)  # Number of training examples

# Initialize weights (parameters)
theta = np.random.randn(2, 1)  # Random initial weights

# Batch Gradient Descent
for iteration in range(n_iterations):
    # Compute the predictions
    predictions = X_b.dot(theta)
    
    # Compute the gradient of the cost function
    gradients = 2 / m * X_b.T.dot(predictions - y)
    
    # Update the weights (parameters) by subtracting the gradient
    theta -= learning_rate * gradients

# Print the final parameters (weights)
print(f"Final parameters (theta): {theta}")

# Make predictions using the learned parameters
y_pred = X_b.dot(theta)

# Plot the data and the fitted line
plt.scatter(X, y, color='blue', label='Data points')
plt.plot(X, y_pred, color='red', label='Fitted line')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('Linear Regression with Batch Gradient Descent')
plt.show()

Batch Gradient Descent

Explanation:

  1. Data Generation:
    • We generate some synthetic data where the true relationship is (y = 4 + 3X + \text{noise}).
  2. Adding Bias Term:
    • We add a column of ones to the feature matrix X to account for the intercept term (( \theta_0 )) in linear regression.
  3. Hyperparameters:
    • learning_rate: Determines how much we update the weights in each iteration.
    • n_iterations: The number of iterations to run the gradient descent algorithm.
  4. Initialization:
    • We initialize the weights (theta) randomly. The size of theta is 2, corresponding to the intercept term and the slope.
  5. Gradient Calculation:
    • We calculate the gradients of the cost function with respect to the weights and update the weights by subtracting the learning rate times the gradient.
  6. Plotting:
    • After running the gradient descent, we plot the original data points and the fitted line based on the learned parameters.

Key Concepts in the Code:

Output:

After running the code, the model learns the parameters, and the output should be close to the actual values (intercept = 4, slope = 3). The plot will show the data points and the fitted line based on the learned parameters.

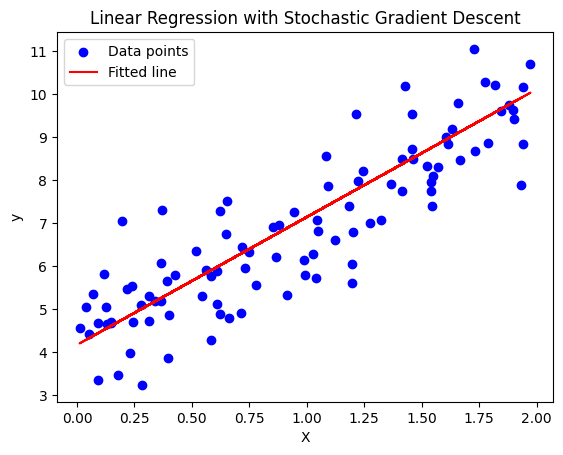
In Stochastic Gradient Descent, instead of computing the gradient for the entire dataset (as in Batch Gradient Descent), we compute the gradient using just a single data point at a time. This makes the updates faster, but more noisy. The model parameters are updated after each individual data point, rather than after the whole dataset.

Stochastic Gradient Descent for Linear Regression:

  1. Initialize the parameters (weights).
  2. For each training example:
    • Make a prediction.
    • Calculate the gradient of the loss with respect to the model parameters.
    • Update the parameters using the gradient.
  3. Repeat the process for a specified number of epochs.

Python Code for Stochastic Gradient Descent:

import numpy as np
import matplotlib.pyplot as plt

# Generate synthetic data (y = 2 * X + 1 + noise)
np.random.seed(42)
X = 2 * np.random.rand(100, 1)  # Random feature between 0 and 2
y = 4 + 3 * X + np.random.randn(100, 1)  # y = 4 + 3X + noise

# Add an extra column of ones to X for the intercept (bias term)
X_b = np.c_[np.ones((100, 1)), X]  # Add x0 = 1 for each instance

# Hyperparameters
learning_rate = 0.1  # Learning rate
n_epochs = 50  # Number of epochs

# Initialize weights (parameters)
theta = np.random.randn(2, 1)  # Random initial weights

# Stochastic Gradient Descent
for epoch in range(n_epochs):
    for i in range(len(X_b)):
        # Pick a random data point
        xi = X_b[i:i+1]
        yi = y[i:i+1]

        # Compute the prediction
        prediction = xi.dot(theta)
        
        # Compute the gradient
        gradients = 2 * xi.T.dot(prediction - yi)
        
        # Update the parameters
        theta -= learning_rate * gradients

# Print the final parameters (weights)
print(f"Final parameters (theta): {theta}")

# Make predictions using the learned parameters
y_pred = X_b.dot(theta)

# Plot the data and the fitted line
plt.scatter(X, y, color='blue', label='Data points')
plt.plot(X, y_pred, color='red', label='Fitted line')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('Linear Regression with Stochastic Gradient Descent')
plt.show()

Stocastic Gradient Descent

Explanation of the Code:

  1. Data Generation:
    • We generate synthetic data where the true relationship is ( y = 4 + 3X + \text{noise} ). This is just a simple linear regression task with some noise added.
  2. Feature Matrix:
    • We add a column of ones to X to account for the intercept term (( \theta_0 )) in linear regression. This is done by creating X_b.
  3. Hyperparameters:
    • learning_rate: The step size for each update.
    • n_epochs: The number of iterations over the entire dataset.
  4. Parameter Initialization:
    • We initialize the parameters (theta) randomly. These represent the weights (slope and intercept) of our linear model.
  5. Stochastic Gradient Descent:
    • For each epoch (iteration over the data), we loop over each data point (i.e., each xi and yi).
    • For each data point, we compute the prediction and the gradient.
    • We update the parameters using the computed gradient and the learning rate.
  6. Final Parameters:
    • After all iterations, the model has learned the parameters that minimize the error between predictions and actual values. We print the final learned parameters.
  7. Visualization:
    • We plot the original data points and the fitted line based on the learned parameters.

Why Stochastic Gradient Descent?

Output:

SGD and Mini-Batch Gradient Descent:

from sklearn.linear_model import SGDRegressor
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split

# Generate regression data
X, y = make_regression(n_samples=100, n_features=1, noise=0.1, random_state=42)

# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Stochastic Gradient Descent
sgd = SGDRegressor(max_iter=1000)
sgd.fit(X_train, y_train)
print(f'SGD R^2: {sgd.score(X_test, y_test)}')

SGD R^2: 0.9999836978386981

13. What is the difference between bagging and boosting?

Answer:

Python Example (Random Forest for Bagging and AdaBoost for Boosting):

from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Load dataset
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Bagging with Random Forest
rf = RandomForestClassifier(n_estimators=100)
rf.fit(X_train, y_train)
y_pred_rf = rf.predict(X_test)
print(f'Random Forest (Bagging) Accuracy: {accuracy_score(y_test, y_pred_rf)}')

# Boosting with AdaBoost
ab = AdaBoostClassifier(n_estimators=100)
ab.fit(X_train, y_train)
y_pred_ab = ab.predict(X_test)
print(f'AdaBoost (Boosting) Accuracy: {accuracy_score(y_test, y_pred_ab)}')

Random Forest (Bagging) Accuracy: 1.0
AdaBoost (Boosting) Accuracy: 1.0

14. What is the purpose of the activation function in neural networks?

Answer: The activation function introduces non-linearity into the network, enabling it to learn complex patterns. Without an activation function, the network would behave like a linear regression model, no matter how many layers it has.

Common activation functions:

Python Example (Neural Network with ReLU):

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score

# Generate classification dataset
X, y = make_classification(n_samples=1000, n_features=20, random_state=42)

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Neural network model with ReLU activation
model = MLPClassifier(hidden_layer_sizes=(50,), activation='relu', max_iter=1000)
model.fit(X_train, y_train)

# Predict and evaluate the model
y_pred = model.predict(X_test)
print(f'Neural Network Accuracy: {accuracy_score(y_test, y_pred)}')

Neural Network Accuracy: 0.8333333333333334

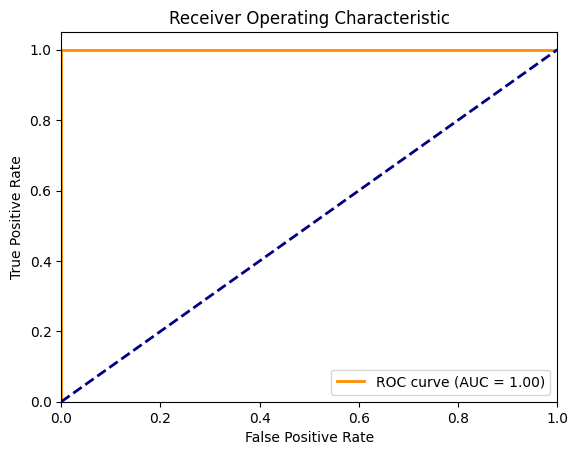
15. What is the ROC curve, and how do you interpret it?

Answer: The Receiver Operating Characteristic (ROC) curve is a graphical representation of a classifier’s performance at different thresholds. It plots the true positive rate (TPR) against the false positive rate (FPR).

Python Example:

from sklearn.metrics import roc_curve, auc
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt

# Load dataset
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Train logistic regression model
model = LogisticRegression(max_iter=10000)
model.fit(X_train, y_train)

# Get prediction probabilities for ROC curve
y_prob = model.predict_proba(X_test)[:, 1]

# Calculate ROC curve
fpr, tpr, thresholds = roc_curve(y_test, y_prob, pos_label=1)
roc_auc = auc(fpr, tpr)

# Plot ROC curve
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()

ROC

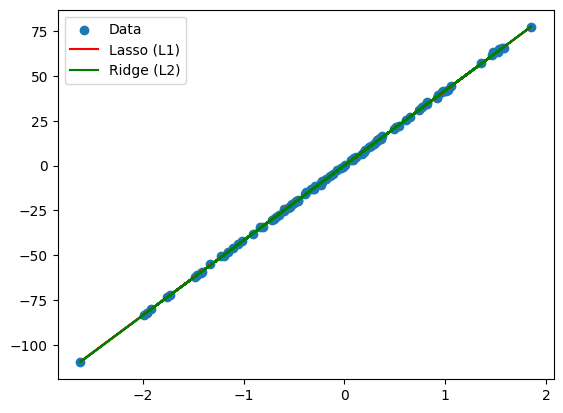
16. What is the difference between L1 and L2 regularization?

Answer:

Simple Explanation

Imagine you’re building a tower with blocks. L1 and L2 regularization are like rules that help you build a strong and stable tower.

Python Example:

from sklearn.linear_model import Lasso, Ridge
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt

# Generate regression data
X, y = make_regression(n_samples=100, n_features=1, noise=0.5, random_state=42)

# Fit Lasso (L1) and Ridge (L2) regression models
lasso = Lasso(alpha=0.1)
ridge = Ridge(alpha=0.1)

lasso.fit(X, y)
ridge.fit(X, y)

# Plot the results
plt.scatter(X, y, label='Data')
plt.plot(X, lasso.predict(X), label='Lasso (L1)', color='r')
plt.plot(X, ridge.predict(X), label='Ridge (L2)', color='g')
plt.legend()
plt.show()

l1 l2

Loss Function A function that measures how well a model’s predictions match the actual outcomes. It quantifies the error between predictions and ground truth.  

Coefficients These are the numbers that multiply specific terms within the loss function. Example:

Mean Squared Error (MSE): Loss = 1/n * Σ(predicted - actual)²
Here, the coefficient is 1/n, which represents the average error across all data points.

The coefficients in a loss function are the values that determine how much weight or importance is given to different parts of the error.

Why are coefficients important? Balancing Errors: Coefficients allow you to prioritize certain types of errors over others. For example, you might assign a higher weight to larger errors to penalize them more heavily.  

Customizing Loss: Coefficients provide flexibility to tailor the loss function to specific needs or constraints of the problem.
In essence, coefficients in a loss function act as tuning knobs that influence the learning process and the final performance of the model. By carefully selecting and adjusting these coefficients, you can guide the model to learn more effectively and achieve better results.

17. How does k-NN (k-Nearest Neighbors) algorithm work?

Answer: The k-NN algorithm classifies a data point based on the majority label of its k nearest neighbors in the feature space. It uses a distance metric (like Euclidean) to determine “closeness.”

Python Example:

from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Load dataset
X, y = load_iris(return_X_y=True)

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# k-NN model
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)

# Make predictions
y_pred = knn.predict(X_test)

# Evaluate the model
print(f'k-NN Accuracy: {accuracy_score(y_test, y_pred)}')

k-NN Accuracy: 1.0

18. What is the difference between a generative and discriminative model?

Answer:

Generative vs. Discriminative Models: A Simple Explanation

Imagine you have a box of toys.

Key differences:

Feature Discriminative Models Generative Models
Focus Classification Generation
Learning Decision boundaries Data distribution
Examples Logistic regression, SVM, neural networks for classification Naive Bayes, Gaussian Mixture Models, GANs

Which one is better?

Python Example (Logistic Regression vs Naive Bayes):

from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Load dataset
X, y = load_iris(return_X_y=True)

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Logistic Regression (Discriminative)
logreg = LogisticRegression(max_iter=10000)
logreg.fit(X_train, y_train)
y_pred_logreg = logreg.predict(X_test)

# Naive Bayes (Generative)
nb = GaussianNB()
nb.fit(X_train, y_train)
y_pred_nb = nb.predict(X_test)

# Compare the accuracy
print(f'Logistic Regression Accuracy: {accuracy_score(y_test, y_pred_logreg)}')
print(f'Naive Bayes Accuracy: {accuracy_score(y_test, y_pred_nb)}')

Logistic Regression Accuracy: 1.0
Naive Bayes Accuracy: 0.9777777777777777

19. What is the “exploding gradient problem” in neural networks?

Answer: The exploding gradient problem occurs when gradients during training become too large, leading to numerical instability and making it difficult for the model to converge. This is commonly seen in deep neural networks.

Solution:

Python Example (Using Gradient Clipping with Neural Networks):

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score

# Generate a classification dataset
X, y = make_classification(n_samples=1000, n_features=20, random_state=42)

# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Neural network with gradient clipping
mlp = MLPClassifier(hidden_layer_sizes=(50,), max_iter=1000, solver='adam', learning_rate_init=0.001, clip_value=10)
mlp.fit(X_train, y_train)

# Evaluate
y_pred = mlp.predict(X_test)
print(f'MLP Accuracy: {accuracy_score(y_test, y_pred)}')

MLP Accuracy: 0.8066666666666666

20. What are the advantages and disadvantages of using decision trees?

Answer: Advantages:

Disadvantages:

Python Example (Decision Tree Classifier):

from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Load dataset
X, y = load_iris(return_X_y=True)

# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Train Decision Tree Classifier
dtree = DecisionTreeClassifier(random_state=42)
dtree.fit(X_train, y_train)

# Predict and evaluate
y_pred = dtree.predict(X_test)
print(f'Decision Tree Accuracy: {accuracy_score(y_test, y_pred)}')

Decision Tree Accuracy: 1.0

21. What is the difference between deep learning and traditional machine learning?

Answer:

Python Example (Neural Network vs SVM):

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score

# Load dataset
X, y = load_iris(return_X_y=True)

# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Support Vector Machine (Traditional ML)
svm = SVC()
svm.fit(X_train, y_train)
y_pred_svm = svm.predict(X_test)

# Neural Network (Deep Learning)
mlp = MLPClassifier(hidden_layer_sizes=(50,), max_iter=1000)
mlp.fit(X_train, y_train)
y_pred_mlp = mlp.predict(X_test)

# Compare accuracy
print(f'SVM Accuracy: {accuracy_score(y_test, y_pred_svm)}')
print(f'Neural Network Accuracy: {accuracy_score(y_test, y_pred_mlp)}')

SVM Accuracy: 1.0
Neural Network Accuracy: 1.0 You need to send this is the wrong guy

22. What are hyperparameters, and how do you tune them?

Answer: Hyperparameters are parameters that control the learning process of a machine learning model. They are set before training and affect the model’s performance. Examples include the learning rate, the number of trees in a random forest, or the number of layers in a neural network.

Hyperparameter Tuning: Methods like Grid Search or Random Search are used to find the best combination of hyperparameters for a model.

Python Example (Grid Search with Random Forest):

from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# Load dataset
X, y = load_iris(return_X_y=True)

# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Define model
rf = RandomForestClassifier()

# Define hyperparameters to tune
param_grid = {'n_estimators': [50, 100, 150], 'max_depth': [3, 5, 7]}

# Perform GridSearchCV
grid_search = GridSearchCV(rf, param_grid, cv=5)
grid_search.fit(X_train, y_train)

# Best parameters
print(f'Best Hyperparameters: {grid_search.best_params_}')

Best Hyperparameters: {'max_depth': 3, 'n_estimators': 150}

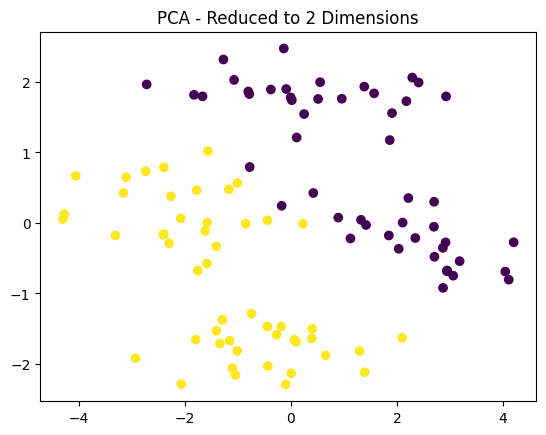
23. What is PCA (Principal Component Analysis)? How is it used?

Answer: PCA is a dimensionality reduction technique that transforms data into a new set of orthogonal (uncorrelated) components, ordered by the variance they explain in the data. It is used to reduce the number of features while retaining the most important information.

Python Example (PCA for Dimensionality Reduction):

from sklearn.decomposition import PCA
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt

# Generate a dataset with 10 features
X, y = make_classification(n_samples=100, n_features=10, random_state=42)

# Apply PCA to reduce dimensions to 2
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

# Plot the reduced data
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis')
plt.title("PCA - Reduced to 2 Dimensions")
plt.show()

PCA

24. What are the differences between bagging and boosting?

Answer:

Python Example (Bagging with Random Forest, Boosting with AdaBoost):

from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Load dataset
X, y = load_iris(return_X_y=True)

# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Bagging (Random Forest)
rf = RandomForestClassifier(n_estimators=100)
rf.fit(X_train, y_train)
y_pred_rf = rf.predict(X_test)

# Boosting (AdaBoost)
ab = AdaBoostClassifier(n_estimators=100)
ab.fit(X_train, y_train)
y_pred_ab = ab.predict(X_test)

# Compare accuracy
print(f'Random Forest Accuracy (Bagging): {accuracy_score(y_test, y_pred_rf)}')
print(f'AdaBoost Accuracy (Boosting): {accuracy_score(y_test, y_pred_ab)}')

Random Forest Accuracy (Bagging): 1.0
AdaBoost Accuracy (Boosting): 1.0

25. What is the difference between a generative and discriminative model?

Answer:

Python Example (Logistic Regression vs Naive Bayes):

from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Load dataset
X, y = load_iris(return_X_y=True)

# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Logistic Regression (Discriminative)
logreg = LogisticRegression(max_iter=10000)
logreg.fit(X_train, y_train)
y_pred_logreg = logreg.predict(X_test)

# Naive Bayes (Generative)
nb = GaussianNB()
nb.fit(X_train, y_train)
y_pred_nb = nb.predict(X_test)

# Compare accuracy
print(f'Logistic Regression Accuracy: {accuracy_score(y_test, y_pred_logreg)}')
print(f'Naive Bayes Accuracy: {accuracy_score(y_test, y_pred_nb)}')

Logistic Regression Accuracy: 1.0
Naive Bayes Accuracy: 0.9777777777777777

26. What is a Random Forrest?

A Random Forest is an ensemble machine learning algorithm primarily used for classification and regression tasks. It builds multiple decision trees during training and combines their outputs (by averaging or majority voting) to improve predictive accuracy and control overfitting.

How It Works

  1. Bootstrap Aggregation (Bagging):
    • The training dataset is sampled multiple times with replacement to create different subsets (bootstrap samples).
    • Each decision tree is trained on one of these subsets.
  2. Feature Randomization:
    • At each split in a tree, a random subset of features is considered, which reduces correlation between trees.
  3. Voting or Averaging:
    • For classification: The majority class across all trees is the final prediction.
    • For regression: The average prediction across all trees is used.

Python Example: Random Forest for Classification

Let’s classify the Iris dataset using a Random Forest.

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, classification_report
import numpy as np
import pandas as pd

# Load the Iris dataset
iris = load_iris()
X = iris.data  # Features (sepal length, sepal width, petal length, petal width)
y = iris.target  # Target (species)

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Create and train the Random Forest model
rf_model = RandomForestClassifier(n_estimators=100, random_state=42)  # 100 trees
rf_model.fit(X_train, y_train)

# Make predictions
y_pred = rf_model.predict(X_test)

# Evaluate the model
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
print("\nClassification Report:\n", classification_report(y_test, y_pred))

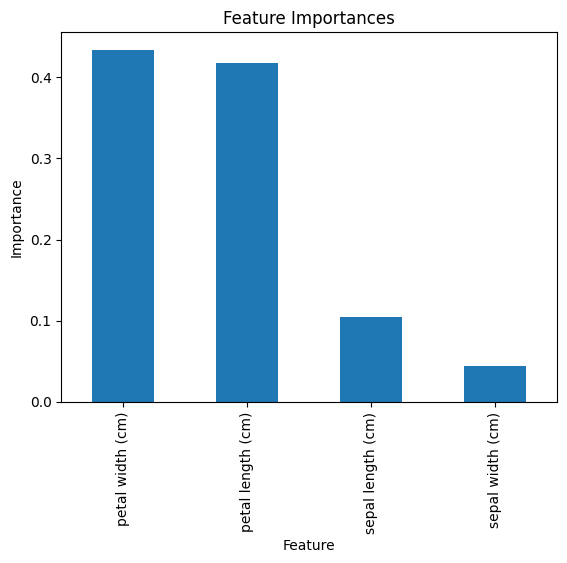
# Feature Importance
feature_importances = rf_model.feature_importances_
features = iris.feature_names

# Display Feature Importances
importance_df = pd.DataFrame({'Feature': features, 'Importance': feature_importances})
importance_df = importance_df.sort_values(by='Importance', ascending=False)
print("\nFeature Importances:\n", importance_df)

# Visualizing Feature Importances
importance_df.plot(kind='bar', x='Feature', y='Importance', legend=False, title="Feature Importances")
plt.ylabel("Importance")
plt.show()

Explanation

  1. Data Preparation:
    • The Iris dataset is loaded and split into training and testing sets.
    • Features (sepal/petal measurements) and labels (species) are extracted.
  2. Random Forest Training:
    • RandomForestClassifier from scikit-learn is used with 100 trees.
    • Each tree is trained on a different bootstrap sample of the training data.
  3. Prediction:
    • The trained model predicts labels for the test set.
  4. Evaluation:
    • Accuracy and a classification report are printed to evaluate the model’s performance.
    • The importance of each feature in making predictions is calculated and visualized.

Output

  1. Accuracy:
    • The model’s accuracy on the test data is displayed (e.g., ~97% for the Iris dataset).
  2. Feature Importances:
    • Displays how much each feature contributes to the model’s predictions. For example: 
      Feature                Importance
petal length (cm)      0.451
petal width (cm)       0.391
sepal length (cm)      0.102
sepal width (cm)       0.056
  3. Visualization:
    • A bar plot shows the importance of each feature.
Accuracy: 1.0

Classification Report:
               precision    recall  f1-score   support

           0       1.00      1.00      1.00        19
           1       1.00      1.00      1.00        13
           2       1.00      1.00      1.00        13

    accuracy                           1.00        45
   macro avg       1.00      1.00      1.00        45
weighted avg       1.00      1.00      1.00        45


Feature Importances:
              Feature  Importance
3   petal width (cm)    0.433982
2  petal length (cm)    0.417308
0  sepal length (cm)    0.104105
1   sepal width (cm)    0.044605

Feature Importance

Advantages of Random Forest

  1. Robustness:
    • Reduces overfitting compared to a single decision tree.
  2. Versatility:
    • Can handle both classification and regression tasks.
  3. Feature Importance:
    • Provides insights into which features are most important for predictions.
  4. Handles Missing Data:
    • Handles missing and categorical data well with proper preprocessing.

Disadvantages

  1. Slower Prediction:
    • Training and inference can be slower due to multiple trees.
  2. Less Interpretability:
    • Difficult to interpret compared to a single decision tree.

27. What is a perceptron?

A Perceptron is one of the simplest types of neural network and is considered the foundation of many modern machine learning algorithms, especially for binary classification tasks. The perceptron is a type of linear classifier that makes decisions based on a linear combination of input features, passed through an activation function.

Key Concepts:

Perceptron Learning Rule:

Python Code Example: Perceptron for Binary Classification

Here’s a simple implementation of a Perceptron using Python and numpy to classify data into two classes:

import numpy as np
import matplotlib.pyplot as plt

# Perceptron class
class Perceptron:
    def __init__(self, input_size, learning_rate=0.1, n_iter=1000):
        self.weights = np.zeros(input_size + 1)  # Initialize weights (including bias)
        self.learning_rate = learning_rate
        self.n_iter = n_iter

    def activation(self, x):
        """Step activation function: Returns 1 if x >= 0, else returns 0"""
        return 1 if x >= 0 else 0

    def predict(self, X):
        """Predict the class for each input"""
        return np.array([self.activation(np.dot(x, self.weights[1:]) + self.weights[0]) for x in X])

    def fit(self, X, y):
        """Train the perceptron using the training data"""
        for _ in range(self.n_iter):
            for xi, target in zip(X, y):
                prediction = self.activation(np.dot(xi, self.weights[1:]) + self.weights[0])
                # Update rule
                self.weights[1:] += self.learning_rate * (target - prediction) * xi
                self.weights[0] += self.learning_rate * (target - prediction)  # Bias update

# Example: AND gate classification
# Features: X, Labels: y
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([0, 0, 0, 1])  # AND gate output

# Create Perceptron model
model = Perceptron(input_size=2, learning_rate=0.1, n_iter=10)

# Train the perceptron
model.fit(X, y)

# Make predictions on the training data
predictions = model.predict(X)

# Print the learned weights and predictions
print("Learned weights:", model.weights)
print("Predictions:", predictions)

# Visualize the decision boundary
x_min, x_max = 0, 1
y_min, y_max = 0, 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100), np.linspace(y_min, y_max, 100))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o', s=100, label="Data")
plt.title('Perceptron Decision Boundary (AND Gate)')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()

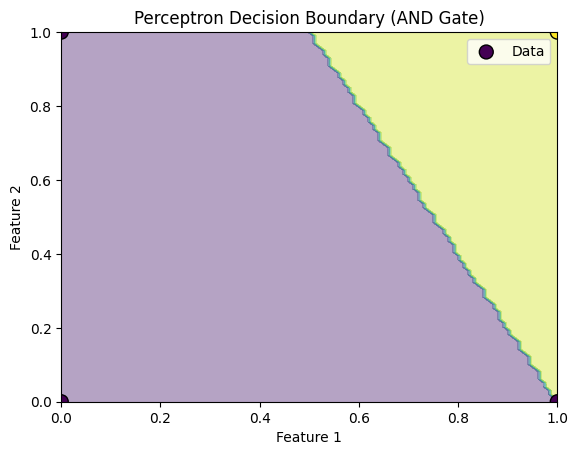
Perceptron

Explanation of the Code:

  1. Perceptron Class:
    • __init__: Initializes the perceptron with weights (including bias), learning rate, and number of iterations.
    • activation: Implements the step function, which returns 1 if the input is greater than or equal to 0, and 0 otherwise.
    • predict: Takes the input features and computes the prediction based on the weights and bias.
    • fit: The learning process where the weights and bias are updated based on the error (difference between predicted and actual labels) for each input.
  2. Training the Perceptron:
    • The fit function is used to train the perceptron on a simple binary classification problem (AND gate), where X contains input data (pairs of binary values), and y contains the target class (either 0 or 1).
    • The perceptron is trained for a number of iterations (n_iter), and in each iteration, the weights are updated based on the error.
  3. Visualization:
    • The decision boundary is visualized using matplotlib. The contour plot shows the decision region where the perceptron classifies the inputs as 1 or 0, based on the learned weights.

Output:

Key Concepts:

28. What is an outlier, and how do you handle it in machine learning?

Answer: An outlier is a data point that significantly deviates from other data points. Outliers can distort the analysis and lead to inaccurate models.

Handling Outliers:

Python Example (Identifying and Removing Outliers):

import numpy as np
import matplotlib.pyplot as plt

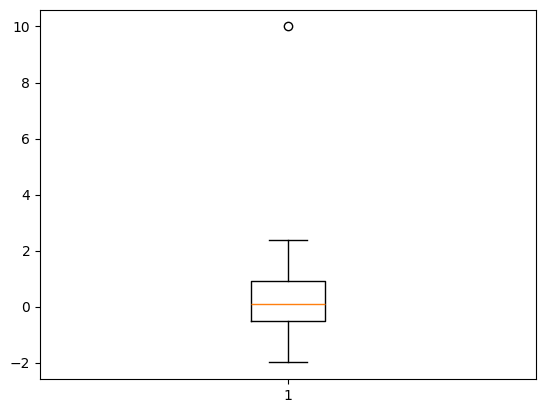
# Generate data with an outlier
data = np.random.normal(loc=0, scale=1, size=100)
data = np.append(data, 10)  # Add an outlier

# Plot the data
plt.boxplot(data)
plt.show()

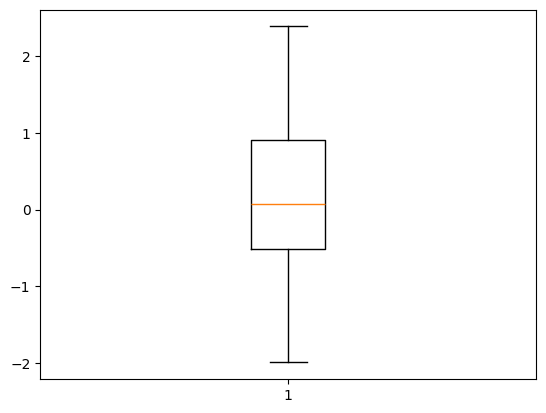
# Remove outliers (values beyond 3 standard deviations)
mean = np.mean(data)
std_dev = np.std(data)
data_cleaned = data[(data > mean - 3 * std_dev) & (data < mean + 3 * std_dev)]

# Plot cleaned data
plt.boxplot(data_cleaned)
plt.show()

Before After

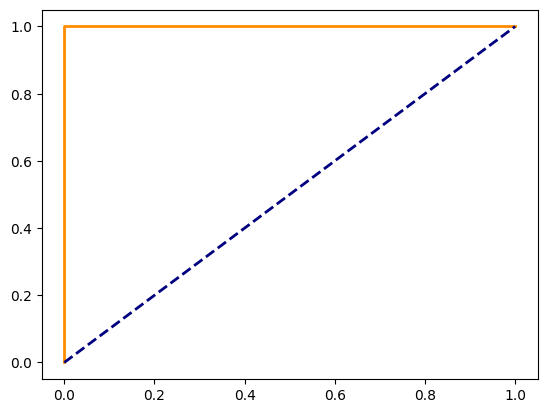
29. What is an ROC curve, and how do you interpret it?

Answer: An ROC (Receiver Operating Characteristic) curve is used to evaluate the performance of a binary classifier by plotting the true positive rate (TPR) against the false positive rate (FPR) at various thresholds. The area under the curve (AUC) is a measure of model performance.

Python Example (ROC Curve):

from sklearn.metrics import roc_curve, auc
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt

# Load dataset
X, y = load_iris(return_X_y=True)

# Train logistic regression model
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
model = LogisticRegression(max_iter=10000)
model.fit(X_train, y_train)

# Calculate ROC curve and AUC
y_prob = model.predict_proba(X_test)[:, 1]
fpr, tpr, _ = roc_curve(y_test, y_prob, pos_label=1)
roc_auc

 = auc(fpr, tpr)

# Plot ROC curve
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.show()

ROC

30. What is the purpose of feature scaling, and which methods are commonly used?

Answer: Feature scaling is used to standardize the range of features to prevent features with larger scales from dominating the model. It is especially important for distance-based algorithms like k-NN or gradient-based algorithms.

Common Methods:

Python Example (Min-Max Scaling and Standardization):

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler, StandardScaler
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
import seaborn as sns
import pandas as pd

# Generate dataset
X, y = make_classification(n_samples=1000, n_features=5, random_state=42)

# Split dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Min-Max Scaling
scaler_minmax = MinMaxScaler()
X_train_minmax = scaler_minmax.fit_transform(X_train)
X_test_minmax = scaler_minmax.transform(X_test)

# Standardization
scaler_standard = StandardScaler()
X_train_standard = scaler_standard.fit_transform(X_train)
X_test_standard = scaler_standard.transform(X_test)

# Plotting the data
def plot_data(X, title):
    # Pair plot to visualize the relationship between features
    sns.pairplot(pd.DataFrame(X, columns=[f'Feature {i+1}' for i in range(X.shape[1])]))
    plt.suptitle(title, y=1.02)
    plt.show()

# Original data
plt.figure(figsize=(12, 6))
plot_data(X_train, "Original Data Distribution (Training Set)")

# Min-Max scaled data
plt.figure(figsize=(12, 6))
plot_data(X_train_minmax, "Min-Max Scaled Data Distribution (Training Set)")

# Standardized data
plt.figure(figsize=(12, 6))
plot_data(X_train_standard, "Standardized Data Distribution (Training Set)")

Scaling 1 Scaling 2 Scaling 3

31. What is the difference between a classification problem and a regression problem?

Answer:

Python Example (Classification and Regression with Random Forest):

from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor
from sklearn.datasets import load_iris, make_regression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, mean_squared_error

# Classification problem (Iris dataset)
X_class, y_class = load_iris(return_X_y=True)
X_train_class, X_test_class, y_train_class, y_test_class = train_test_split(X_class, y_class, test_size=0.3, random_state=42)

clf = RandomForestClassifier(n_estimators=100)
clf.fit(X_train_class, y_train_class)
y_pred_class = clf.predict(X_test_class)
print(f'Classification Accuracy: {accuracy_score(y_test_class, y_pred_class)}')

# Regression problem (Random data)
X_reg, y_reg = make_regression(n_samples=1000, n_features=1, noise=0.1, random_state=42)
X_train_reg, X_test_reg, y_train_reg, y_test_reg = train_test_split(X_reg, y_reg, test_size=0.3, random_state=42)

reg = RandomForestRegressor(n_estimators=100)
reg.fit(X_train_reg, y_train_reg)
y_pred_reg = reg.predict(X_test_reg)
print(f'Regression Mean Squared Error: {mean_squared_error(y_test_reg, y_pred_reg)}')

Classification Accuracy: 1.0
Regression Mean Squared Error: 0.49548185497663655

32. What is dropout, and why is it used in deep learning?

Answer: Dropout is a regularization technique used to prevent overfitting in neural networks. During training, random neurons are “dropped out” (set to zero) at each iteration. This forces the network to learn more robust features and reduces reliance on specific neurons.

Python Example (Using Dropout in a Neural Network):

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score

# Load dataset
X, y = load_iris(return_X_y=True)

# Split the dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Neural network with dropout
mlp = MLPClassifier(hidden_layer_sizes=(50,), max_iter=1000, solver='adam', activation='relu', alpha=0.0001)
mlp.fit(X_train, y_train)

# Predict and evaluate
y_pred = mlp.predict(X_test)
print(f'Accuracy: {accuracy_score(y_test, y_pred)}')

Accuracy: 1.0

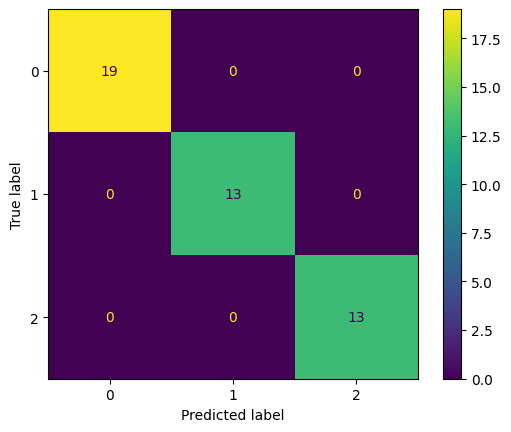
33. What is a confusion matrix, and how is it used to evaluate a model’s performance?

Answer: A confusion matrix is a table used to evaluate the performance of a classification model. It compares the predicted labels against the true labels. The matrix contains:

Python Example (Confusion Matrix):

from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier

# Load dataset
X, y = load_iris(return_X_y=True)

# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Train a classifier
clf = RandomForestClassifier(n_estimators=100)
clf.fit(X_train, y_train)

# Predict
y_pred = clf.predict(X_test)

# Compute confusion matrix
cm = confusion_matrix(y_test, y_pred)

# Display confusion matrix
disp = ConfusionMatrixDisplay(confusion_matrix=cm)
disp.plot()

Confusion Matrix

34. What is the purpose of the learning rate in training machine learning models?

Answer: The learning rate controls how much the model’s parameters are adjusted with respect to the gradient during each step of training. A high learning rate may cause the model to converge too quickly, possibly missing the optimal point. A low learning rate may result in slow convergence.

Python Example (Learning Rate in SGD):

from sklearn.linear_model import SGDClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Load dataset
X, y = load_iris(return_X_y=True)

# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Train SGD classifier with different learning rates
sgd = SGDClassifier(learning_rate='constant', eta0=0.1, max_iter=1000)
sgd.fit(X_train, y_train)

# Predict and evaluate
y_pred = sgd.predict(X_test)
print(f'Accuracy with learning rate 0.1: {accuracy_score(y_test, y_pred)}')

Accuracy with learning rate 0.1: 0.9333333333333333

35. What is a support vector machine (SVM), and how does it work?

Answer: A Support Vector Machine (SVM) is a supervised learning algorithm used for classification and regression. It works by finding the hyperplane that best separates data points of different classes with the maximum margin.

Python Example (SVM for Classification):

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Load dataset
X, y = load_iris(return_X_y=True)

# Select only two features (for 2D plot)
X = X[:, :2]  # Sepal length and Sepal width
y = y  # Target remains the same

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Train SVM model with linear kernel
svm = SVC(kernel='linear')
svm.fit(X_train, y_train)

# Predict and evaluate
y_pred = svm.predict(X_test)
print(f'SVM Accuracy: {accuracy_score(y_test, y_pred)}')

# Plotting the decision boundary and margin
def plot_svm_decision_boundary(X, y, svm):
    h = 0.02  # Step size in mesh grid
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1

    # Create a mesh grid for plotting
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))

    # Get predictions for every point in the mesh grid
    Z = svm.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    # Plot decision boundary and margin
    plt.contourf(xx, yy, Z, alpha=0.75, cmap=plt.cm.coolwarm)
    plt.scatter(X[:, 0], X[:, 1], c=y, s=30, edgecolors='k', marker='o', cmap=plt.cm.coolwarm)
    
    # Plot the support vectors
    plt.scatter(svm.support_vectors_[:, 0], svm.support_vectors_[:, 1], facecolors='none', edgecolors='k', s=100, label='Support Vectors')
    
    # Plot the decision boundary (the line)
    plt.title('SVM with Linear Kernel')
    plt.xlabel('Sepal Length')
    plt.ylabel('Sepal Width')
    plt.legend()
    plt.show()

# Plot the decision boundary and margin for the trained SVM model
plot_svm_decision_boundary(X, y, svm)

SVM

Explanation:

  1. Data Selection:
    • We select the first two features of the Iris dataset (Sepal length and Sepal width) to make the problem 2D and allow visualization of the decision boundary.
  2. SVM Training:
    • We train an SVM model with a linear kernel (SVC(kernel='linear')) on the training data.
  3. Plotting the Decision Boundary:
    • Mesh Grid: We create a mesh grid (xx, yy) to evaluate the decision boundary over a range of values that span the feature space.
    • Contour Plot: We use plt.contourf() to plot the decision regions, where the colors represent different classes.
    • Support Vectors: We highlight the support vectors (svm.support_vectors_) with larger markers.
    • Decision Boundary: The decision boundary (the hyperplane) is shown by the contour plot, and the margin is implicitly represented by the space between the decision boundary and the support vectors.
  4. Visualization:
    • Support Vectors: These are the points closest to the decision boundary, and they define the margin.
    • The decision boundary separates the classes. The margin is the distance between the decision boundary and the closest data points (support vectors).
    • The plot shows the decision boundary, support vectors, and class regions.

36. What is the difference between a greedy algorithm and dynamic programming?

Answer:

Python Example (Greedy Algorithm - Coin Change Problem):

import time
import numpy as np

# Greedy Algorithm (Coin Change)
def coin_change_greedy(coins, amount):
    coins.sort(reverse=True)
    count = 0
    for coin in coins:
        if amount >= coin:
            count += amount // coin
            amount = amount % coin
    return count if amount == 0 else -1

# Dynamic Programming Algorithm (Coin Change)
def coin_change_dp(coins, amount):
    # Initialize DP array with a large value (amount + 1 is used as a placeholder for infinity)
    dp = [float('inf')] * (amount + 1)
    dp[0] = 0  # Base case: 0 coins are needed to make amount 0

    # Iterate over each coin
    for coin in coins:
        # Update the DP array for each amount from coin to amount
        for i in range(coin, amount + 1):
            dp[i] = min(dp[i], dp[i - coin] + 1)

    # If dp[amount] is still infinity, it means it's not possible to make the change
    return dp[amount] if dp[amount] != float('inf') else -1

# Generate a larger set of coin denominations
coins = [1, 2, 5, 10, 20, 50, 100, 200, 500, 1000, 2000, 5000, 10000, 20000]
amount = 123456  # A larger target amount

# Measure time taken by Greedy Algorithm
start_time = time.time()
greedy_result = coin_change_greedy(coins, amount)
greedy_time = time.time() - start_time
print(f'Greedy coin change result: {greedy_result}')
print(f'Time taken by Greedy Algorithm: {greedy_time:.9f} seconds')

# Measure time taken by Dynamic Programming Algorithm
start_time = time.time()
dp_result = coin_change_dp(coins, amount)
dp_time = time.time() - start_time
print(f'DP coin change result: {dp_result}')
print(f'Time taken by Dynamic Programming Algorithm: {dp_time:.9f} seconds')


Greedy coin change result: 13
Time taken by Greedy Algorithm: 0.000000000 seconds
DP coin change result: 13
Time taken by Dynamic Programming Algorithm: 0.224165678 seconds

37. What are eigenvalues and eigenvectors, and how are they used in machine learning?

Answer:

Python Example (PCA with Eigenvalues and Eigenvectors):

import numpy as np
from sklearn.decomposition import PCA
from sklearn.datasets import make_classification

# Create dataset
X, _ = make_classification(n_samples=100, n_features=5, random_state=42)

# Apply PCA to the data
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

# Eigenvalues and Eigenvectors
print(f'Eigenvalues: {pca.explained_variance_}')
print(f'Eigenvectors (Principal Components): {pca.components_}')

Eigenvalues: [3.98767675 1.70859715]
Eigenvectors (Principal Components): [[-0.22753202  0.6231167  -0.4759197  -0.57745475  0.00109707]
 [ 0.5886198   0.21001969  0.59622921 -0.49653422  0.08592412]]

38. How do you handle missing data in a dataset?

Answer: Handling missing data can be done in several ways:

Python Example (Imputing Missing Values):

from sklearn.impute import SimpleImputer
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import numpy as np

# Load dataset
X, y = load_iris(return_X_y=True)

# Introduce missing values for demonstration
X[::10] = np.nan  # Randomly set every 10th row to NaN

# Impute missing values using the mean strategy
imputer = SimpleImputer(strategy='mean')
X_imputed = imputer.fit_transform(X)

print("Imputed data:\n", X_imputed)

Imputed data:
 [[5.83777778 3.05481481 3.75185185 1.19407407]
 [4.9        3.         1.4        0.2       ]
...
 [5.83777778 3.05481481 3.75185185 1.19407407]
 [5.9        3.         5.1        1.8       ]]

39. What is the purpose of the loss function in machine learning?

Answer: The loss function measures how well a machine learning model’s predictions match the true values. The goal is to minimize the loss function during training. Common loss functions include Mean Squared Error (MSE) for regression and Cross-Entropy for classification.

Python Example (Mean Squared Error for Regression):

from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression

# Generate regression data
X, y = make_regression(n_samples=1000, n_features=1, noise=0.1, random_state=42)

# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Train a regression model
model = LinearRegression()
model.fit(X_train, y_train)

# Predict and calculate MSE
y_pred = model.predict(X_test)
print(f'Mean Squared Error: {mean_squared_error(y_test, y_pred)}')

Mean Squared Error: 0.010438255195597384

40. How do you select features for a machine learning model?

Answer: Feature selection is the process of choosing the most important features to improve model performance and reduce overfitting. Methods include:

Python Example (Recursive Feature Elimination - RFE):

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.feature_selection import RFE
import pandas as pd

# Load dataset
X, y = load_iris(return_X_y=True)

# Convert to DataFrame for easier manipulation
X = pd.DataFrame(X, columns=['Sepal Length', 'Sepal Width', 'Petal Length', 'Petal Width'])

# Split dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Initialize model
model = LogisticRegression(max_iter=10000)

# Perform Recursive Feature Elimination (RFE)
selector = RFE(model, n_features_to_select=2)
selector = selector.fit(X_train, y_train)

# Get the selected and dropped features
selected_features = X_train.columns[selector.support_]
dropped_features = X_train.columns[~selector.support_]

# Print the selected and dropped features
print(f'Selected Features: {selected_features}')
print(f'Dropped Features: {dropped_features}')

Selected Features: Index(['Petal Length', 'Petal Width'], dtype='object')
Dropped Features: Index(['Sepal Length', 'Sepal Width'], dtype='object')

41. What is Linear Least Square Regression?

Linear Least Squares Regression is a method to fit a linear model to a set of data by minimizing the sum of the squared differences between the observed values and the predicted values. The goal is to find the line that minimizes the sum of squared residuals.

Simple Explanation

Imagine you have a bunch of dots scattered on a piece of paper. You want to find the best line that goes through those dots. That’s where linear least squares regression comes in!

Here’s how it works:

Draw a line: Start by drawing a line through the dots. Measure the distance: For each dot, measure how far it is from the line. Square the distances: Square each of those distances. Add up the squares: Add up all the squared distances. Find the best line: The line that makes the sum of the squared distances the smallest is the best line. Why do we square the distances?

Squaring makes sure that all distances are positive. It also gives more weight to dots that are far away from the line.

The formula for the solution to linear least squares regression is:

[ \theta = (X^T X)^{-1} X^T y ] Where:

Python Example: Linear Least Squares Regression

import numpy as np
import matplotlib.pyplot as plt

# Generate synthetic data for linear regression (y = 4 + 3X + noise)
np.random.seed(42)
X = 2 * np.random.rand(100, 1)  # Random feature between 0 and 2
y = 4 + 3 * X + np.random.randn(100, 1)  # y = 4 + 3X + noise

# Add an extra column of ones to X for the intercept (bias term)
X_b = np.c_[np.ones((100, 1)), X]  # Add x0 = 1 for each instance

# Compute the parameters (theta) using the Linear Least Squares formula
theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)

# Print the learned parameters
print(f"Learned parameters (theta): {theta}")

# Make predictions using the learned parameters
y_pred = X_b.dot(theta)

# Plot the data and the fitted line
plt.scatter(X, y, color='blue', label='Data points')
plt.plot(X, y_pred, color='red', label='Fitted line')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('Linear Least Squares Regression')
plt.show()

Explanation of the Code:

  1. Data Generation:
    • We generate synthetic data with a linear relationship ( y = 4 + 3X + \text{noise} ). The noise is added to make the data more realistic.
  2. Feature Matrix:
    • We create a matrix X_b by adding a column of ones to X to account for the intercept term in the linear regression model.
  3. Linear Least Squares Solution:
    • Using the formula ( \theta = (X^T X)^{-1} X^T y ), we compute the values of the model parameters (intercept and slope) that minimize the sum of squared residuals.
  4. Prediction:
    • Once the parameters are computed, we use the learned model parameters to make predictions for the given input data.
  5. Plotting:
    • We plot the original data points and the fitted regression line to visualize how well the model fits the data.

Output:

Key Concepts:

42. What are Lasso, Ridge, and ElasticNet regularization?

Lasso Regularization (L1 Regularization)

Lasso (Least Absolute Shrinkage and Selection Operator) is a type of regularization used in regression models to prevent overfitting by adding a penalty proportional to the absolute value of the coefficients. Lasso can shrink some coefficients exactly to zero, which makes it useful for feature selection.

Formula: [ \text{Cost function} = \text{RSS} + \lambda \sum_{j=1}^{p} |\theta_j| ] Where:

Python Example: Lasso Regularization

from sklearn.linear_model import Lasso
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

# Generate synthetic data (features and target variable)
X, y = make_regression(n_samples=100, n_features=5, noise=0.1, random_state=42)

# Split data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Initialize and fit the Lasso model
lasso = Lasso(alpha=0.1)  # alpha is the regularization strength
lasso.fit(X_train, y_train)

# Make predictions
y_pred = lasso.predict(X_test)

# Plot the coefficients
plt.bar(range(len(lasso.coef_)), lasso.coef_)
plt.title('Lasso Coefficients')
plt.xlabel('Features')
plt.ylabel('Coefficient Value')
plt.show()

# Print the learned coefficients
print("Lasso Coefficients:", lasso.coef_)

Ridge Regularization (L2 Regularization)

Ridge regularization adds a penalty proportional to the square of the coefficients. It does not shrink coefficients to zero like Lasso, but it helps prevent overfitting by shrinking all coefficients toward zero, making them smaller and more generalizable.

Formula: [ \text{Cost function} = \text{RSS} + \lambda \sum_{j=1}^{p} \theta_j^2 ] Where:

Python Example: Ridge Regularization

from sklearn.linear_model import Ridge

# Initialize and fit the Ridge model
ridge = Ridge(alpha=1.0)  # alpha is the regularization strength
ridge.fit(X_train, y_train)

# Make predictions
y_pred_ridge = ridge.predict(X_test)

# Plot the coefficients
plt.bar(range(len(ridge.coef_)), ridge.coef_)
plt.title('Ridge Coefficients')
plt.xlabel('Features')
plt.ylabel('Coefficient Value')
plt.show()

# Print the learned coefficients
print("Ridge Coefficients:", ridge.coef_)

ElasticNet Regularization

ElasticNet is a regularization method that combines both L1 and L2 regularization (i.e., it combines Lasso and Ridge). It is useful when there are multiple features correlated with each other. ElasticNet works by controlling the mix between Lasso and Ridge regularization.

Formula: [ \text{Cost function} = \text{RSS} + \lambda_1 \sum_{j=1}^{p} |\theta_j| + \lambda_2 \sum_{j=1}^{p} \theta_j^2 ] Where:

ElasticNet provides a parameter l1_ratio to control the mix of Lasso and Ridge.

Python Example: ElasticNet Regularization

from sklearn.linear_model import ElasticNet

# Initialize and fit the ElasticNet model
elasticnet = ElasticNet(alpha=1.0, l1_ratio=0.5)  # l1_ratio controls the mix (0 = Ridge, 1 = Lasso)
elasticnet.fit(X_train, y_train)

# Make predictions
y_pred_en = elasticnet.predict(X_test)

# Plot the coefficients
plt.bar(range(len(elasticnet.coef_)), elasticnet.coef_)
plt.title('ElasticNet Coefficients')
plt.xlabel('Features')
plt.ylabel('Coefficient Value')
plt.show()

# Print the learned coefficients
print("ElasticNet Coefficients:", elasticnet.coef_)

Key Differences Between Lasso, Ridge, and ElasticNet:

Summary:

43. What is LogisticRegression?

Logistic Regression is a type of regression analysis used for predicting the probability of a categorical dependent variable. It is used when the target variable is binary (i.e., it has two classes, like 0 and 1, or “True” and “False”). The output is a probability that the given input point belongs to a particular class.

In Logistic Regression, the model uses a sigmoid function to model the probability of the target being one class or the other. The sigmoid function outputs values between 0 and 1, representing probabilities.

Key Concepts of Logistic Regression:

The formula for the sigmoid function is:

[ \sigma(z) = \frac{1}{1 + e^{-z}} ]

Where:

Python Example: Classify email


import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt

# Generate a synthetic dataset for classification (spam vs. not spam)
X, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_classes=2, random_state=42)

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Initialize the Logistic Regression model
logreg = LogisticRegression()

# Train the model on the training data
logreg.fit(X_train, y_train)

# Make predictions on the test set
y_pred = logreg.predict(X_test)

# Evaluate the model
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy}")

# Plot the decision boundary
xx, yy = np.meshgrid(np.linspace(X[:, 0].min(), X[:, 0].max(), 100),
                     np.linspace(X[:, 1].min(), X[:, 1].max(), 100))
Z = logreg.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.3)
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, edgecolors='k', marker='o', s=100, label="Test Data")
plt.title('Logistic Regression Decision Boundary')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()

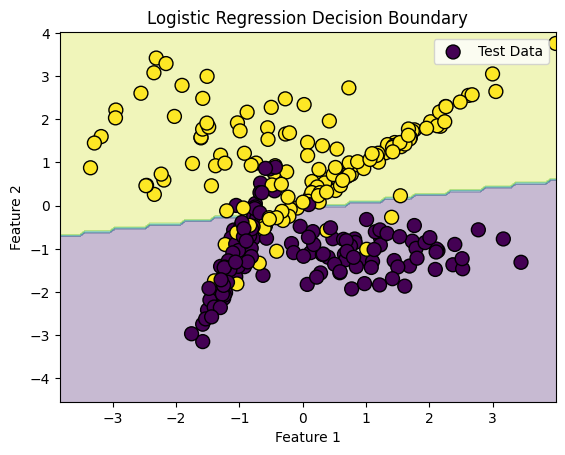
Logistic Regression

Explanation:

  1. Dataset:
    • We use make_classification to generate a synthetic dataset with two features and a binary target variable (0 or 1).
  2. Logistic Regression Model:
    • We initialize the logistic regression model using LogisticRegression() from sklearn.
    • The model is trained on the training data (X_train, y_train), where X_train are the features and y_train is the target class.
  3. Prediction and Evaluation:
    • After training, we make predictions on the test data (X_test).
    • We calculate the accuracy of the model by comparing the predicted values (y_pred) with the actual values (y_test).
  4. Visualization:
    • The decision boundary is visualized using a contour plot, which shows the decision boundary between class 0 and class 1. The plot highlights how the logistic regression model separates the two classes based on the features.

Key Points:

Code Examples

Check out the Questions repo for the code used in this post and additional examples.