ernanhughes

+++ date = ‘2025-01-16T00:21:05Z’ title = ‘Cellular Automata: Introduction’ categories = [‘ca’] tag = [‘ca’] +++

Summary

This page is the first in a series of posts about Cellular Automata.

I believe that we could get the first evidence of AI through cellular automata.

A recent paper Intelligence at the Edge of Chaos found that LLM’s trained on more complex data generate better results. Which makes sense in a human context like the harder the material is I study the smarter I get. We need to find out why this is also the case with machines. The conjecture of this paper is that creating intelligence may require only exposure to complexity.

There are some properties of Cellular Automata that I believe make them contenders for early emergence.

By the end of this series we will know a lot more about Cellular Automata and hopefully why they apprear to be intelligent.

What Are Cellular Automata?

Cellular automata(CA) are mathematical model that consist of a grid of cells, where each cell can be in one of a finite number of states. These states evolve over time according to simple rules based on the states of neighboring cells.

Components of Cellular Automata:

Key Concepts

Why Are Cellular Automata Interesting?

Types of Cellular Automata

There are various types of cellular automata, each with unique characteristics and applications:

Conway’s Game of Life

The Game of Life demonstrates how complex and unpredictable patterns can arise from a set of very simple rules. This concept of emergence is fundamental to understanding how complex systems can arise from simple interactions. It bridges the gap between abstract computation (theoretical computer science) and physical systems.

Setup

Despite these simple rules, it produces surprisingly complex and lifelike patterns.

import numpy as np
import matplotlib.pyplot as plt

# Constants
N = 100  # Grid size
ON = 255  # Value for live cells
OFF = 0  # Value for dead cells
NUM_SNAPSHOTS = 4  # Number of snapshots to display
OUTPUT_FILENAME = "game_of_life_snapshots.png"  # File name for the PNG

# Initialize grid with random on/off values
def initialize_grid(size, on_prob=0.2):
    return np.random.choice([ON, OFF], size * size, p=[on_prob, 1 - on_prob]).reshape(size, size)

# Compute the next state of the grid
def update_grid(grid):
    new_grid = grid.copy()
    for i in range(N):
        for j in range(N):
            # Compute the sum of the 8 neighbors using toroidal boundary conditions
            neighbors = (
                grid[i, (j - 1) % N] + grid[i, (j + 1) % N] +
                grid[(i - 1) % N, j] + grid[(i + 1) % N, j] +
                grid[(i - 1) % N, (j - 1) % N] + grid[(i - 1) % N, (j + 1) % N] +
                grid[(i + 1) % N, (j - 1) % N] + grid[(i + 1) % N, (j + 1) % N]
            ) / 255

            # Apply Conway's rules
            if grid[i, j] == ON:
                if neighbors < 2 or neighbors > 3:
                    new_grid[i, j] = OFF
            else:
                if neighbors == 3:
                    new_grid[i, j] = ON
    return new_grid

# Generate multiple snapshots of the grid
def generate_snapshots(grid, num_steps):
    snapshots = [grid]
    for _ in range(num_steps - 1):
        grid = update_grid(grid)
        snapshots.append(grid)
    return snapshots

# Plot snapshots side by side and save as PNG
def plot_snapshots(snapshots, output_filename=None):
    num_snapshots = len(snapshots)
    fig, axes = plt.subplots(1, num_snapshots, figsize=(15, 5))

    for i, ax in enumerate(axes):
        ax.matshow(snapshots[i], cmap="binary")
        ax.set_title(f"Step {i}")
        ax.axis("off")

Game of life

1d Cellular Automata

Setup

A 1D cellular automaton consists of:

Rules

1. The Neighborhood

2. Total Number of Configurations

For binary states (0 or 1), the number of possible configurations of a neighborhood is:

[ 2^{\text{Neighborhood Size}} = 2^3 = 8 ]

Each configuration maps to a new state (0 or 1), leading to (2^8 = 256) possible rules for a radius-1, binary-state 1D cellular automaton.

3. Rule Representation

Rules are often represented as a binary sequence corresponding to all possible neighborhood configurations. For example, in Rule 30:

Neighborhood 111 110 101 100 011 010 001 000
New State 0 0 0 1 1 1 1 0

This rule is encoded as 00011110 in binary or as 30 in decimal (hence the name Rule 30).

Examples of 1D Cellular Automata Rules

Rule 30

Rule 30 is one of the most famous 1D CA rules, known for its chaotic, unpredictable patterns despite its simple definition. It has been used in random number generation and even cryptography.

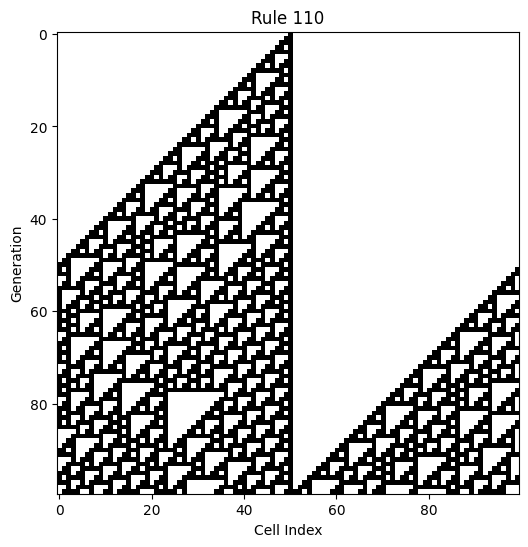
All Rules

Rule 110

Rule 110 is particularly significant because it is Turing complete, meaning it can simulate any computation that a Turing machine can perform.

All Rules

Rule 90

Rule 90 generates a well-known Sierpiński triangle pattern.

Rule 90

<img src="" width="" height="" alt="">

Class to support generation and display of all 1D rules

This class will support genrating and disaplaying all 1D rules 0 -255


import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact, IntSlider
from IPython.display import display

class CellularAutomaton1D:
    def __init__(self, rule_number, size=100, steps=100, init_cond='single'):
        self.rule_number = rule_number  # Rule number (0-255)
        self.size = size                # Number of cells in a generation
        self.steps = steps              # Number of generations to simulate
        self.init_cond = init_cond      # Initial condition ('single', 'random', or custom array)
        self.rule_binary = np.array(self._decimal_to_binary(rule_number))
        self.grid = np.zeros((steps, size), dtype=np.int8)
        self.current_generation = np.zeros(size, dtype=np.int8)
        self._init_first_generation()
    
    def _decimal_to_binary(self, n):
        """Convert a decimal number to an 8-bit binary representation."""
        return np.array([int(x) for x in np.binary_repr(n, width=8)])
    
    def _init_first_generation(self):
        """Initialize the first generation based on the initial condition."""
        if self.init_cond == 'single':
            # Single cell in the middle set to 1
            self.current_generation[self.size // 2] = 1
        elif self.init_cond == 'random':
            # Random initial state
            self.current_generation = np.random.choice([0, 1], size=self.size)
        elif isinstance(self.init_cond, np.ndarray) and len(self.init_cond) == self.size:
            # Custom initial state provided as an array
            self.current_generation = self.init_cond.copy()
        else:
            raise ValueError("Invalid initial condition.")
        self.grid[0] = self.current_generation.copy()
    
    def _get_neighborhood(self, i):
        """Get the neighborhood of cell i with periodic boundary conditions."""
        left = self.current_generation[(i - 1) % self.size]
        center = self.current_generation[i]
        right = self.current_generation[(i + 1) % self.size]
        return left, center, right
    
    def _apply_rule(self, neighborhood):
        """Determine the new state of a cell based on its neighborhood and the rule."""
        # Convert the neighborhood to an index (0-7)
        idx = 7 - int(''.join(str(bit) for bit in neighborhood), 2)
        return self.rule_binary[idx]
    
    def run(self):
        """Run the cellular automaton simulation."""
        for step in range(1, self.steps):
            new_generation = np.zeros(self.size, dtype=np.int8)
            for i in range(self.size):
                neighborhood = self._get_neighborhood(i)
                new_state = self._apply_rule(neighborhood)
                new_generation[i] = new_state
            self.current_generation = new_generation
            self.grid[step] = self.current_generation.copy()
    
    def get_grid(self):
        return self.grid
    
    def display(self):
        """Display the simulation results."""
        plt.figure(figsize=(12, 6))
        plt.imshow(self.grid, cmap='binary', interpolation='nearest')
        plt.title(f'Rule {self.rule_number}')
        plt.xlabel('Cell Index')
        plt.ylabel('Generation')
        plt.show()

Display all rules

These functions will generate all the rules and display them as an image


def generate_all_automata(size=40, steps=40, init_cond='single'):
    automata_grids = []
    for rule_number in range(256):
        ca = CellularAutomaton1D(rule_number=rule_number, size=size, steps=steps, init_cond=init_cond)
        ca.run()
        grid = ca.get_grid()
        automata_grids.append(grid)
    return automata_grids


def display_all_automata(automata_grids, items_per_row=10, output_filename="all_rules.png"):
    total_automata = len(automata_grids)
    num_rows = total_automata // items_per_row
    if total_automata % items_per_row != 0:
        num_rows += 1

    fig, axes = plt.subplots(num_rows, items_per_row, figsize=(items_per_row * 1.5, num_rows * 1.5))
    # Increase hspace to add more vertical space between rows
    plt.subplots_adjust(wspace=0.1, hspace=0.5)

    for idx, grid in enumerate(automata_grids):
        row = idx // items_per_row
        col = idx % items_per_row
        if num_rows > 1:
            ax = axes[row, col]
        else:
            ax = axes[col]
        ax.imshow(grid, cmap='binary', interpolation='nearest')
        ax.set_title(f'Rule {idx}', fontsize=8)
        ax.axis('off')

    # Hide any unused subplots
    for idx in range(total_automata, num_rows * items_per_row):
        row = idx // items_per_row
        col = idx % items_per_row
        if num_rows > 1:
            ax = axes[row, col]
        else:
            ax = axes[col]
        ax.axis('off')

    plt.savefig(output_filename, dpi=300)
    plt.show()

# Generate and display all automata
automata_grids = generate_all_automata(size=100, steps=100, init_cond='single')
display_all_automata(automata_grids, items_per_row=8)

All Rules

Code Examples

Check out the ca notebooks for the code used in this post and additional examples.